The size of a classical screening design is influenced by design resolution and geometric symmetry, whereas the size of a definitive screening design grows in proportion with the number of factors.
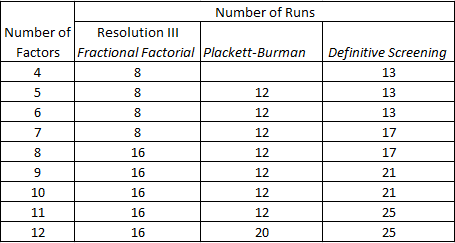
The smallest classical screening designs, and the ones most efficient at handling a large number of factors are Resolution III designs. The table below compares the size of these designs with a DSD with the same number of factors:
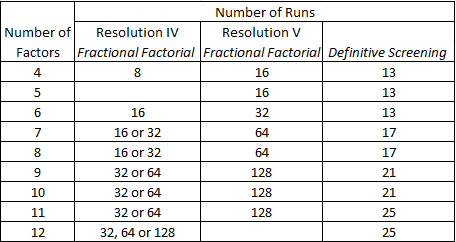
DSDs are larger than these classical designs, however, the DSDs are designed to overcome the limitations of Resolution III designs, namely the ambiguity that arises from the confounding between main effects and two-factor interactions. With classical designs resolving the ambiguity usually requires a follow-on experiment or constructing a design with higher resolution. So let’s take a look at the size of higher resolution designs:
The size of a factorial design is constrained by a requirement that the number of runs is a power of 2. This makes it unwieldy for a large number of factors. DSDs don’t suffer this problem, the number of runs grows in relation to the number of factors.
At a theoretical level a DSD has (2f+1) runs where f is the number of factors. As shown in the above numbers this is not the case in the JMP implementation of the designs. The number of runs for an odd number of factors is 2 higher than the theoretical figure. My guess is that designs with an odd number of factors have been created with a dummy factor in order to improve their statistical properties (DSDs with an even number of factors appear to have a more desirable aliasing structure).
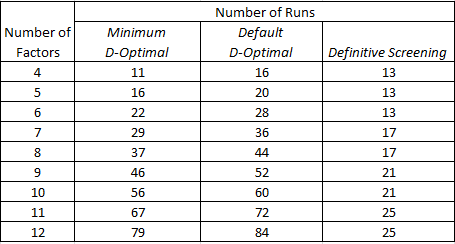
Next I want to compare the size of a DSD with a custom design. The number of runs associated with a custom design is determined in the first instance by the model specification. The tabulation below is based on a model containing all two-factor interactions:
DSDs are not small, they are ultra-small! They are supersaturated in the sense that the number of estimable effects is greater than the number of runs. We all want small designs of course, but that inevitably requires some trade-offs. In subsequent posts I’ll be taking a closer look at what can be estimated, how well they can be estimated, and what challenges there may be in the analysis of the data.