Capability Indices and Process Shift

In this post I will derive a simple relationship between process shift and the capability indices Cp and Cpk.

Introduction

The process capability statistic Cp compares process variation against the width of a process operating window:

$C_p =$ $\frac{U - L}{6 \sigma}$

where U and L are the upper and lower specification limits respectively, and σ represents the standard deviation of the process variation.

In order to take account of process location the ratio is extended to include process mean $\overline Y$ :

$C_{pu} =$ $\frac{U - \overline Y}{3 \sigma}$ $C_{pl} =$ $\frac{\overline Y - L}{3 \sigma}$

& $C_{pk} =$ Min $(C_{pu},C_{pl})$

So now we can confidently talk about process capability in terms of the indices Cp and Cpk. But it seems to me that this is convenient shorthand at the expense of transparency.

For example, if I am given values for Cp and Cpk the underlying process shift is not necessarily obvious.

Cp / Cpk and Process Shift

Whilst the relationship between process shift and capability indices is not immediately apparent there is nonetheless a simple relationship:

$\Delta =$ $3 \sigma (C_p - C_{pk})$

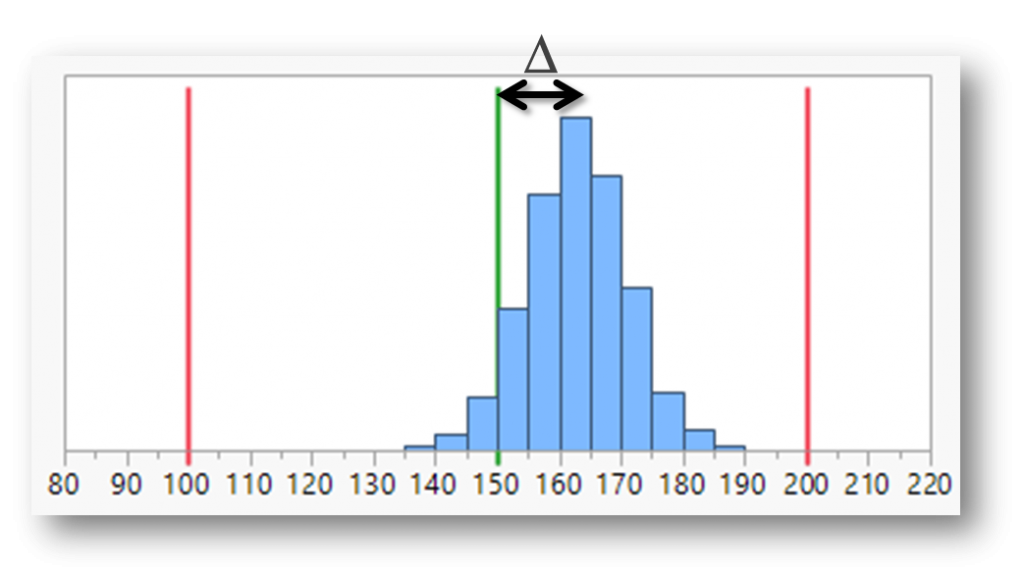
where the shift Δ is measured as the distance of the process mean from the target.

The rest of this post looks at the derivation of this result.

The Algebra

Let’s assume without loss of generality that the process shift is positive (with respect to the target T). Then:

$C_{pk} = C_{pu} =$ $\frac{U - \overline Y}{3 \sigma}$

The process shift is $(\overline Y-T)$ so we need an appropriate expression for and $\overline Y$ and $T$ .

An Expression for $\overline Y$

From the above expression:

$3 \sigma C_{pk} = U - \overline Y$

which implies

$\overline Y = U - 3 \sigma C_{pk}$

An Expression for 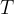$T$

If we assume that the specs are symmetric then

$T=$ $\frac{U + L}{2}$

which implies

$L = 2 T - U$

but also

$C_p =$ $\frac{U - L}{6 \sigma}$

therefore

$C_p$ $= \frac{U - (2T - U)}{6 \sigma} = \frac{2(U - T)}{6 \sigma}$

this implies

$U - T = 3 \sigma C_p$

therefore

$T = U - 3 \sigma C_p$

An Expression for Process Shift

Using the above expressions for $T$ and $\overline Y$ an expression for process shift can be constructed and simplified:

$\Delta = \overline Y - T = (U - 3 \sigma C_{pk}) - (U - 3 \sigma C_p)$

$= 3 \sigma(C_p - C_{pk})$

In Summary

In this post I have derived a simple relationship between process shift and the capability indices Cp and Cpk. Given the simplicity of the relationship, my derivation feels somewhat laboured – perhaps you know of a more direct method?

JMP Ahead