I have been investigating the use of logistic regression to model image pixel data. Now I want to take a look at the use of neural networks. In this post I am going to build the simplest possible neural network and compare it against a simple logistic regression.
Pixel 543
Let me introduce pixel 543:
This was the first pixel to be selected when I performed a stepwise regression. I’m going to use this as a single term in my model to help predict whether an image contains the hand written digit ‘5’ or ‘6’.
I want to build a neural network using this variable, but to give the model some context I will first look at a model build using logistic regression.
Logistic Regression Model
I’ve already taken an in-depth look at building a logistic model with a single predictor and multiple predictor variables, so I will keep this short. I just want something that I can use for comparative purposes.
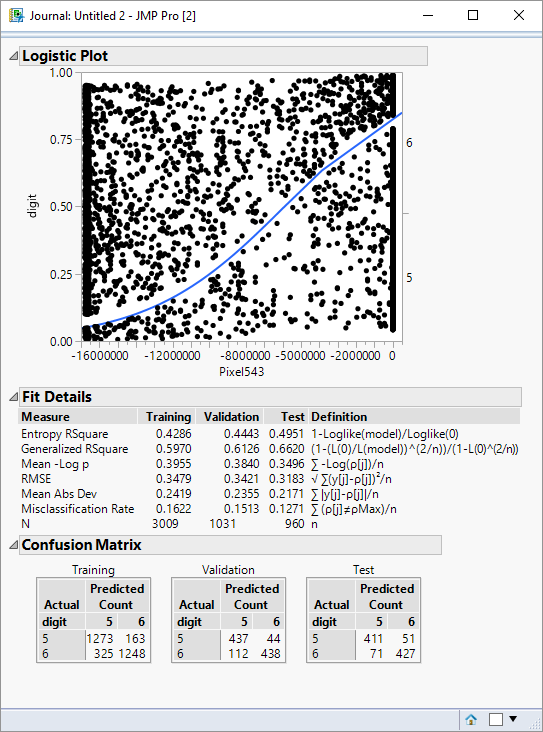
The output below summarises the key features that I am interested in:
The graph shows the distinctive S-curve of the logistic function. The pixel is a number coded as an RGB value. As an integer it appears large negative when it is “on” and zero when it is “off”. The graph indicates that when the pixel is off there is a high probability that the image represents a ‘5’; when the pixel is on there is a very high probability that the image represents a ‘6’.
The confusion matrices show how successful the data is classified with respect to the training, validation and test partitions. The misclassification values are summarised in the Fit Details outline as a misclassification rate.
If I focus on the validation partition, the misclassification rate is about 15%. I saw from stepwise regression that I can drive the miscassifcation rate down to about 3%, but this is pretty good performance for a single pixel!
Building a Neural Network
A neural network is a network of nodes that take inputs and transform them into outputs. The transformation takes a particular form (shape) and is tuned by selecting appropriate weights for the inputs.
I’m going to build the simplest possible network – a single node, and I will specify that the transformation shape should be a logistic function:
The process of fitting the neural network model will select an optimal value for the weight for the input into the node. That weight is equivalent to the parameter estimate associated with a logistic regression.
Here is what the model specification looks like in JMP:
This screenshot is based on JMP Pro, but the way I have specified the model doesn’t rely on any pro-specific features. The neural network consists of a single TanH node.
TanH ?
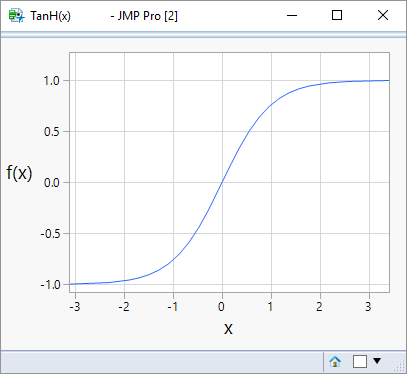
I said I was going to use a node that applied a logistic transformation, instead I have selected a hyperbolic tangent. This is the definition of tanH:
Not particularly helpful right? Maybe a picture will help:
 created using code from this blog post.
created using code from this blog post.
Whereas the logistic function produces a response from 0 to 1, this function produces a response constrained to the range -1 to +1. It’s the same as the logistic model except for a scaling factor – it will still perform the tasks of converting a continuous input variable into a score that can be used to make a classification.
The Results
There are implementation differences between a neural network and a logistic regression, so for the same data we can’t expect identical results but we they ought to be comparable if the model forms are the same.
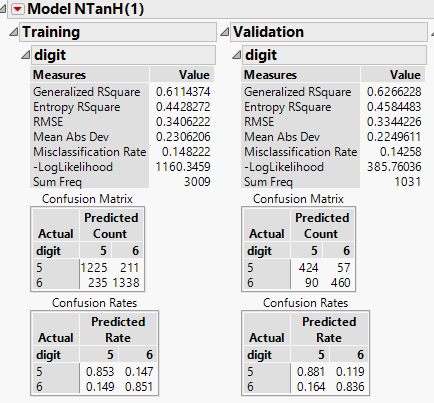
Here are the results for the training and validation partitions:
The validation misclassification rate is 14.3% (similar to the 15.1% reported by the logistic regression).
Equivalence
What I have wanted to show, was that a very simple neural network is equivalent to a logistic regression. If instead of a binary response I had a continuous one, then I could have chosen a linear node in my network and it would have been equivalent to a linear regression.
A network with a single node is somewhat trivial and doesn’t really justify the “network” descriptor, so I want to incrementally introduce additional complexity. That will be the theme of subsequent posts.