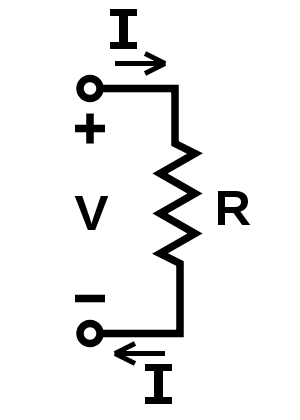
I have results from an experiment.
It is an investigation of a material that can reasonably be expected to obey Ohm’s law.
I have a challenge for you …
I’ve posted 6 lessons on YouTube to help you get started with JSL. You can access the playlist below. And if you’ve worked through all the lessons and would like a final copy of the code you can also download it from here.
When you create a new journal, you are presented with an empty window – which can feel a bit intimidating.
What content should you add, and why?
I take a look at 4 use-cases for JMP Journals …
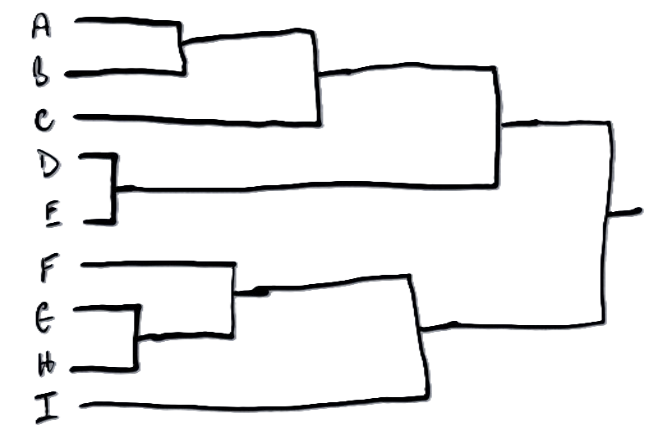
There is only one thing worse than a bad visualisation, and that is a good visualisation that you don’t understand.
So if you have ever gone to a conference and the presenter has used a dendrogram assuming you know how to read it, but you didn’t, then this is for you.
The ability of JMP Software to easily create decision trees makes it a fantastic tool for troubleshooting.
I’m going to share with you 3 tips to increase their effectiveness.
![]()
For 2024, I will give more focus to my YouTube channel.
This means more regular blog posts, supplemented by video content …

I am building a library of functions that I would like to distribute as a single JSL file. But some of my functions reference image files. In this blog post I will explain the process I use for serialising the image file so that it can be embedded directly into my JSL script.
One of the most important tasks that a computer can do it repetition of tasks. That’s why iteration is such an important element of JSL code. In version 16 of JMP, new syntax was introduced to describe the way we iterate over elements of structures such as lists and matrices.
In this post I take a look at how JSL can be used to perform string manipulation.