 Statistics is not about conforming to some strange protocol that we neither agree with nor like.
Statistics is not about conforming to some strange protocol that we neither agree with nor like.
At least it shouldn’t be that way.
We shouldn’t see statistics as some exotic discipline that we tag on to the end of our scientific analysis. For it to add value it needs to be integrated into our workflow, and in order to do that it helps to understand how statisticians see the world. They think differently to scientists, and it really helps to get inside there heads and see the world from their perspective. Let’s see if we can do that.
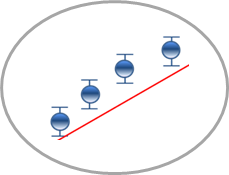
Consider the graph below. Is there lack of fit?
Simplistically, the answer to that question is “yes” or “no”. I can illustrate these two scenarios below.
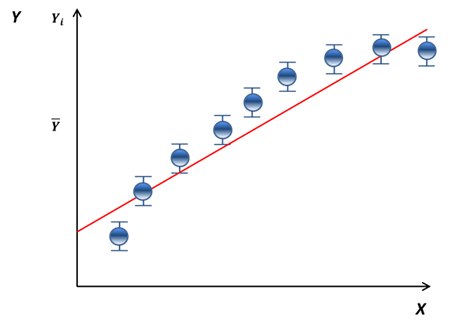
“white-space” between the error bars
and the fitted line suggests lack of fit
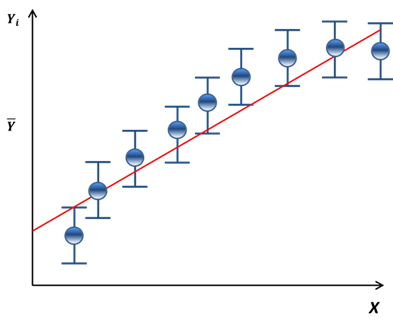
no lack of fit – the fitted line fits
the data points within the margin
of error indicated by the error bars
For the first scenario I may conclude that there is lack of fit and therefore I might want to investigate using a quadratic curve to fit the data. For the second scenario I might conclude that the linear fit is adequate and a quadratic curve would result in over-fitting.
The history of statistical software would suggest that statisticians don’t like error bars on their graphs but their methodology is remarkably similar – just that it is based on numbers and not error bars.
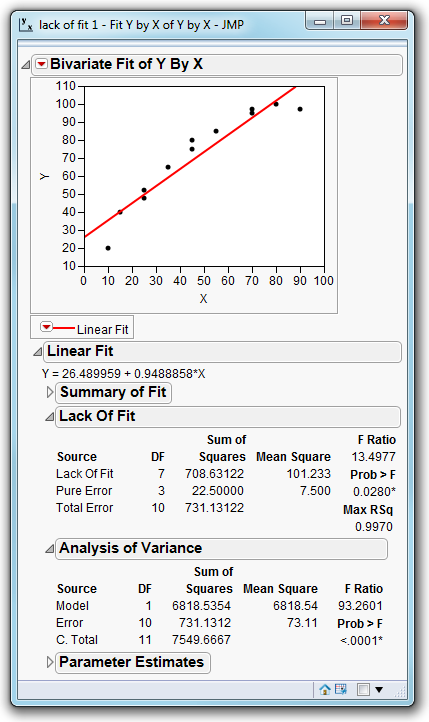
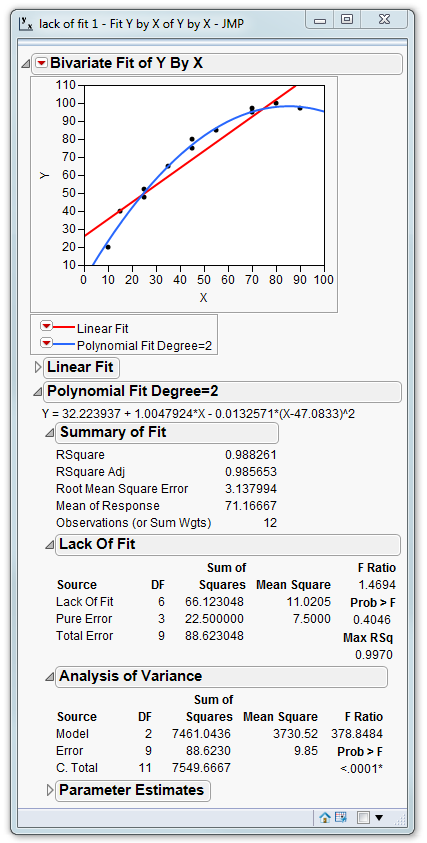
What exactly is the error bar? It gives an indication of the level of variation that we expect to see at the observed data points. In practice it is established by performing repeat measurements for the same value of X. When our data contains these repeat measures JMP automatically provides lack-of-fit information as shown below:
The lack-of-fit table decomposes the total error (variation unexplained by the model) into two components: lack of fit and pure error.
The pure error term is the variation that results from the repeated measures. It represents the error bars on the graphs.
The lack of fit represents the “white-space” between our data points and the fitted line.
To understand how this information is used in the table let’s take a closer look at those error bars:
When we look at the graph containing error bars we use them to help assess whether the line fits within the margin of error. Put another way:
is the “white-space” large or small
relative to the error bars
This is exactly the same question that the statistician is answering with the lack-of-fit table.
When a statistician asks the question “Is A large or small relative to B” he (or she) constructs a ratio A/B. If A is large then the ratio will be “significantly” greater than 1. It is always possible that in “reality” A is not large but we observe a large value by chance simply because of experimental noise. A statistician can quantify this probability – and that is really the only place where we get into tricky stats stuff – the rest of it is just a very slightly different way of describing problems.
So let’s look at our example. The ratio between the white-space and the error bars is 13.4977. I don’t need a statistician to tell me that this number is larger than 1. But could this number have arisen by chance – just because of “noise”. The probability of observing a ratio as large at 13 by chance depends on a number of factors:
- How many data points were used to calculate the fitted line
- How many data points were used to estimate the error bars
- Whether the measurements were independent of each other
Taking all this into account an F-distribution is used to convert the ratio into a probability: 0.0280. This is the probability of the number 13.4977 being observed “by chance”. There is a probability of just under 3% that due to random noise in our measurements we ended up with a set of data that yields a ratio of 13.4977 . More likely then that it occurred because there is curvature in the data.
By using statistics to guide me I can now improve my fit by using a quadratic curve:
At the beginning of this article I suggested that we should seek to embed statistical thinking into our workflow. I can use this example to illustrate what I mean but to do so I need to do a little reverse engineering.
That’s for my next blog entry!
I delight in the info on your websites. Thank you so much!