Did you know that JMP has an LP Solver? Linear programming (LP) is a technique for optimising a function subject to a set of linear constraints. [See here for the Wiki description of linear programming].
The solver takes the form of a function called LPSolve. This can be quite tricky to use, so I wrote a front-end to make the functionality more accessible:
The method is traditionally associated with the field of Operational Research, but if there are any JMP users interested in it, let me know and I can get it posted on the file exchange.
I developed this front-end for my own personal interests. I wanted to explore the use of JMP for Data Envelopment Analysis. That’s still a project on hold for me at the moment, but if any readers have an interest in this topic I’d be keen to hear from you!
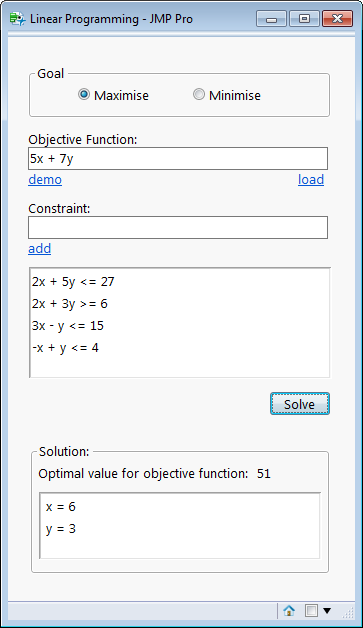
This looks interesting. Do you make your code available somewhere? I’d learn just as much about parsing free-form input as I would about LPSolve. Thanks for showing this!
Hi Casey
I can probably drop the code onto the JMP File Exchange. I’ll just need to check the completeness of the code – it was a project I started for personal interest but never fully completed – so would just need to do a couple of checks on the code before posting it.
I understand what you mean about parsing the free-form input – most of the code was just dealing with allowing a human-readable form of the problem specification that could still be easily processed. As it stands it follows reasonable conventions for defining linear programming problems.
If you have any specific queries about user inputs in JSL, let me know, I’m always interested in fresh topics for my blog!
Thanks for your comments.
Dave
Were you able to upload this to the file exchange? I’ve looked several times but I can’t find it there.
Using LPSolve is proving to be very non-intuitive even for simple cases. Hopefully I’m just overlooking something simple.
For example,
Maximize
143 x +60 y
Subject To
120 x +210 y <= 15000
110 x +30 y <= 4000
x +y <= 75
—————————————————–
A = [120 210, 110 30, 1 1 ];
b = [15000, 4000, 75];
c = [143 60];
L = [0 0];
U = [. .];
neq = 0; nle = 3; nge = 0;
{x, z} = LPSolve( A, b, c, L, U, neq, nle, nge );
Show( x, z );
x = [0, 0];
z = 0; //Uh no…
Correct answer should be
x = 21.875
y = 53.125
Objective function = 6315.63
I can get this if I change to
neq = 0; nle = 1; nge = 2;
x = [21.875, 53.125];
z = 6315.625;
I just don't know why I would need to do so. It seems like nle = 3 from the constraints.
I can graph the linear constraints, make a polygon for the feasibility region, and overlay an isoline or two and easily see the solution. For more than two variables in the objective function a graphical approach will become more difficult if not impossible of course.
Sorry I missed your comment. The code should now be on the file exchange: https://community.jmp.com/docs/DOC-9506
I tried it with your example and it gave the correct answer (with the exception of an annoying rounding error!)
Tack för att dela detta superb hemsida .
Hi Dave,
I’m liking this front end, but wondered how many variables you can use. Your example uses x and y but will it allow a larger number and if so what is the script set up to use as letters? Do you think JMP might put a front end on this functionality at some point?
Thanks!
Claire
Hi Claire
You can find the code on the file exchange: https://community.jmp.com/t5/JMP-Scripts/LP-Solver/ta-p/22794
The code uses pattern matching to parse the text as algebraic delimiters (+, -, etc), numeric coefficients and alphabetic variable names. In principle there is no limit to the number of variables nor their names. I think this is OR functionality rather than stats, so I’m not sure how it would fit into the JMP environment (I presume its accessible at the scripting level because JMP implements various optimisation techniques to aid model interpretation). The JSL function does the job but its not friendly to use, so I wanted to build something that took problem definitions in the nature form that you would expect to express a linear programming problem. You should treat the code as proof of principle that fully robust!
Hi
I don’t know how to use the application
I add some constraint to the app but it didn’t work
For example:
MAX x + y + z
subject to:
x 0
y 0
z 0
The Error Message:
Name Unresolved: op in access or evaluation of ‘op’ , op/*###*/
copy paste error:
MAX x + y + z
subject to:
x <10
y <20
z 0
y>0
z>0
(just test the app using this simple example)
Hi Luke – sorry I didn’t see your messages. If you still have problems let me know and I’ll take a look at it. Regards,