I’m working on some predictive modelling projects and I need to iteratively compute R2 statistics over 100’s of variables. Each time I do the calculations I need to go and have an extended coffee break – and I’m starting to buzz with too much caffeine so I thought I would look to see whether I could make my code more efficient!
Linear regression in matrix form looks like this:
One of the great things about JSL is that I can directly implement this formula:
β = Inv(X`*X)*X`*Y;
Where the grave accent indicates the transpose of the X matrix. That’s it! One line of code to compute the parameter estimates (β) for a set of X and Y data. There’s a direct correspondence between the mathematical form and the code – no need to figure out complex algorithms to convert the problem into JSL. I of course need the matrices, so here is the full code:
// generate matrices
X = Column("height") << Get Values;
Y = Column("weight") << Get Values;
// add a column of 1's for the intercept term
X = J(Nrow(X),1) || X;
// compute least squares estimates
β = Inv(X`*X)*X`*Y;
Now I have my solution I can use it to compute the R2 statistic:
N = NRows(Y); Ybar = Mean(Y); R2 = (β`*X`*Y - N*Ybar^2)/(Y`*Y - N*Ybar^2);
In practice I want to perform this for 100’s of variables based on real-world data. That requires a bit more care to handle situations such as missing data or singular values. Below is a more robust implementation:
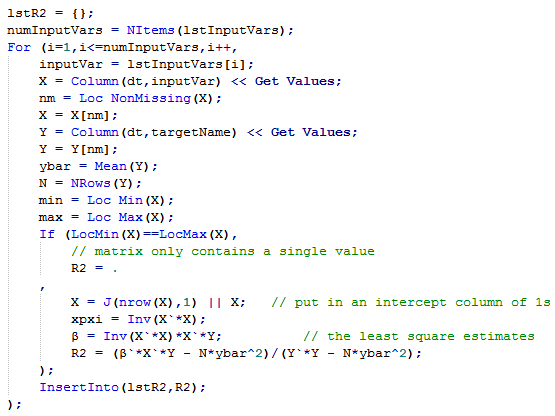
Of course it’s possible to perform regression in JMP using the Bivariate, and in JSL this is how I would extract the R2 value:
biv = Bivariate(
Y( :weight),
X( :height ),
Fit Line, invisible
);
rep = biv << report;
mat = rep[NumberColBox(1)] << Get As Matrix;
rep << Close Window;
R2 = mat[1];
In fact, if my only goal is the calculation of R2 then I could use the Multivariate platform. And then of course there is the Fit Model platform.
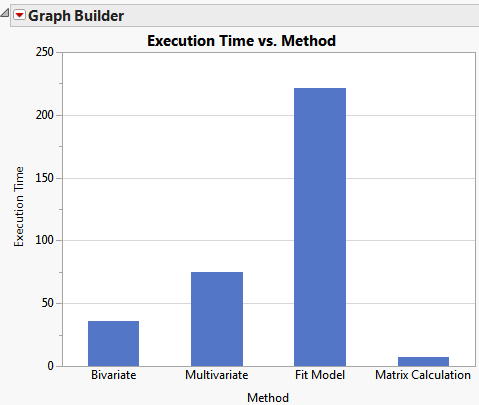
How do these methods compare in terms of performance?
Below is a chart of execution times for each method:
The matrix calculations are 5 times faster than Bivariate and over 30 times faster than Fit Model. That last statistic is important because I also want to generalise the method for some forward selection calculations that involve more than one X variable in the model.
Super Website. Vielen Dank.
thanks for information